Because this single variable K determines the critical torque-tension relationship, the factors that cause its value to vary about 300 percent aren’t clear. The nut factor, as defined in the equation (often called the short-form relationship), is not derived from engineering principles. Instead, it is arrived at experimentally to make the equation valid.
Published test procedures call for tensioning a threaded fastener in a controlled manner, while monitoring both torque and tension. At the prescribed torque or tension value, the nut factor is calculated by inserting T, D and F in the short-form equation and solving for K. Given the unsophisticated nature of the nut factor, one may be surprised to know that there are published torque-tension relationships derived from engineering principles. They produce similar results to one another and take the general form T=XF, where X is a placeholder for a series of terms containing dimensional variables and friction coefficients.
So, if there are more “intelligent” ways of relating torque to tension, why do we insist on using fudge factors? Well, the best answer is that the fudge factor K gives the most accurate result. As with any decision of whether physical testing can be eliminated by numerical analysis, all derived equations are only as good as the assumptions going into the derivations. Accurate results require that all the variables are known and can be measured accurately.
When competent testing of the actual components is practical, the short-form equation will provide the most accurate torque-tension relationship. However, when testing is not in the cards, calculation based on derived relationships with good data gives better results than picking a nut factor from a reference table.
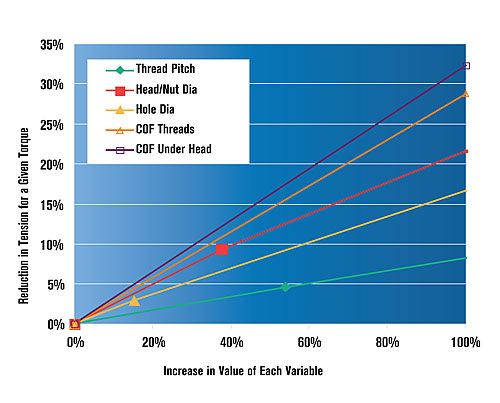
To understand what factors influence the relationship between torque and tension, let’s review the variables contained in the long-form equations and quantify their relative influence. For a given fastener diameter, the primary influences on the relationship between torque and tension are thread pitch (and pitch diameter which varies with it), the head or nut diameter (whichever is rotated), the diameter of the clearance hole, and the coefficients of friction (COF) at the mating threads and between the head or nut and mating material.
Essentially, reaction torques resist the torque input and the long-form equations calculate and sum those resisting torques. How do our design decisions influence torque-tension? The figure above illustrates the effect of doubling the value of each variable. It shows that if the thread COF was doubled while the other variables remained the same, the bolt tension generated for the same installation torque would decrease 29 percent.
While COF values occur on a continuous spectrum, the dimensions of standard fasteners and accompanying clearance holes tend to be discrete. Therefore, the graph also contains three points showing the effect of design alternatives for a single fastener size.
The three intermediate data points show the effect of replacing a fine-thread, hex-head fastener in a close hole with a coarse-thread, hex-flange head fastener in a loose hole. For example, replacing a hex-head fastener with a hex-flange head (but not changing thread pitch or hole diameter) increases the bearing diameter by 37 percent, which in turn will cause bolt tension to be reduced by 9 percent for a given torque. While these values vary a bit depending on fastener size and the long-form equation used, the relative importance of each remains the same. A



