When choosing an encoder for a motion control system, you’ll be faced with numerous technical terms. The amount of data can be overwhelming. Which terms should you focus on first, and which can be deferred? These three concepts deserve your attention: resolution, accuracy and precision.

At first glance, it may seem that all three mean roughly the same thing. You may wonder if they’re interchangeable; indeed, many people speak of them as if they are. After all, if an encoder has high resolution, doesn’t that mean it’s accurate? And if it’s accurate, then it has to be precise, right? The answer to these questions is a firm no.

In fact, the terms are independent of each other. Each refers to a specific encoder characteristic, and they are not interchangeable. To clear up any confusion, we’ll explain what resolution
means for incremental encoders, then note any differences for linear and absolute encoders. We’ll move on to accuracy, and finish with precision. Along the way, we’ll give tips on how to use knowledge about each term to make the best encoder selection, and how to calibrate a system once the encoder is in place.

Resolution

In math, science and engineering, the term resolution specifies the smallest distance that can be measured or observed.

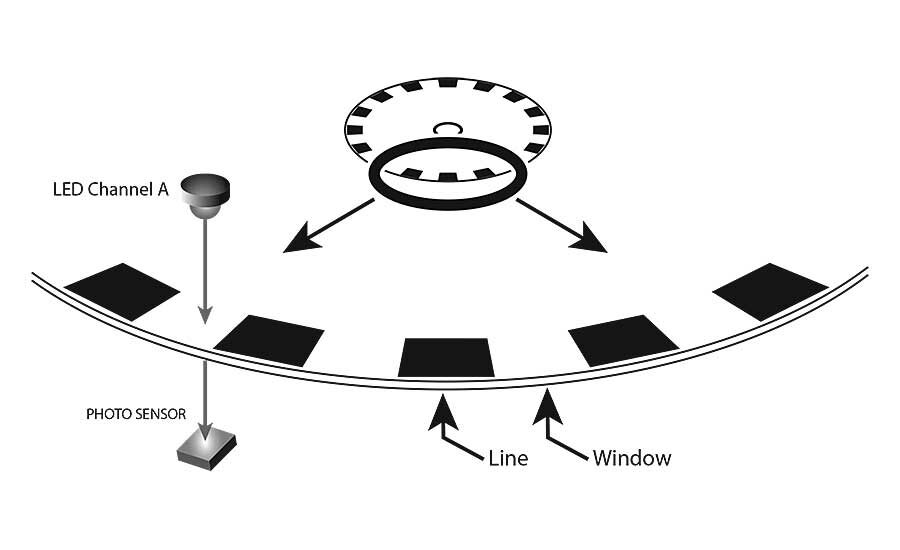
To make an incremental encoder, a manufacturer creates a disk with a pattern on it. The pattern divides the disk into distinct regions. For example, one common pattern consists of lines and windows printed on a
transparent disk.

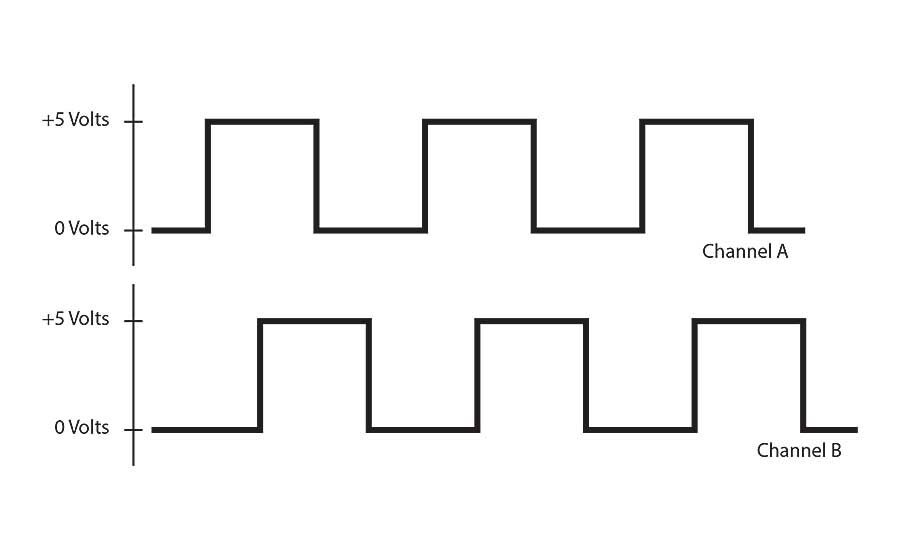
When an LED projects light at the disk, the light strikes either a window or a line. Windows allow light to pass through the disk to a photo sensor on the other side. Lines block the light. As the disk rotates, output from the encoder module—channel A—is a series of high and low signals; their value depends on whether the photo sensor receives light (high) or
not (low).

When applied to optical encoders, resolution specifies the number of times the output signal goes high per revolution. This number can match the number of lines on a disk; or, especially with higher resolutions, it can be a multiple of the number of lines.

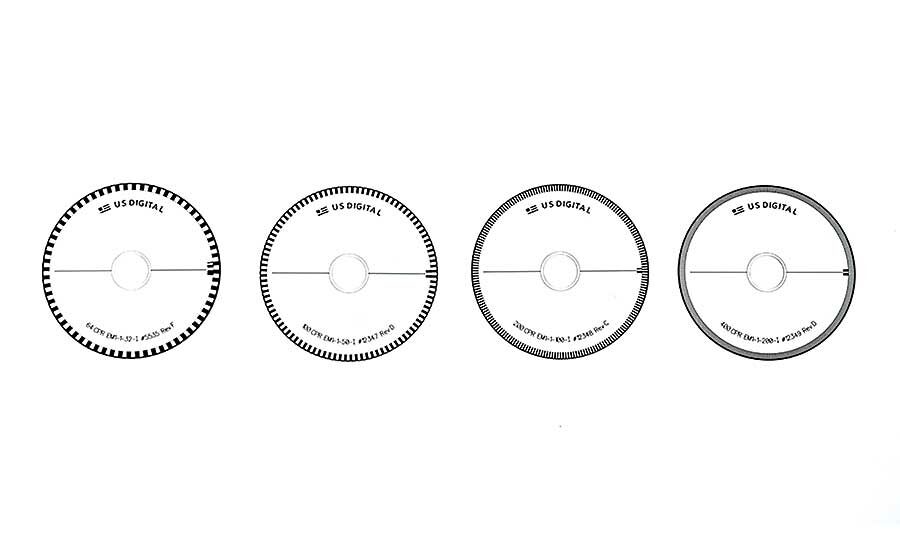
The number of lines on a disk is always related to the resolution. Typical values range from low numbers like 32 or 64 to much higher
resolutions of 5,000 or 10,000 and beyond.

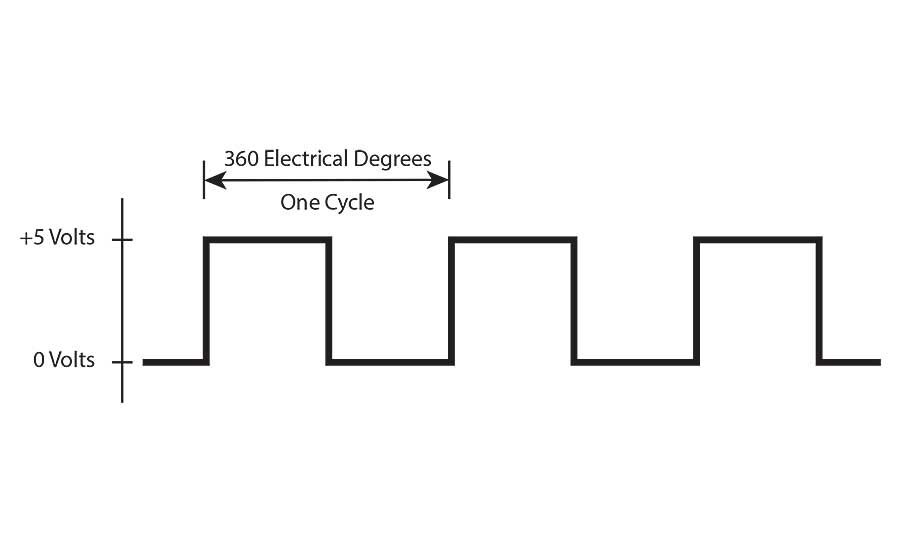
Encoder resolution is measured in units of cycles per revolution (CPR). The word cycle has both a physical and an electrical meaning. Physically, on the disk, a cycle is composed of one line-and-window pair. Therefore, in its most basic form, CPR is the same as the number of lines, the number of windows, or the number of line-and-window pairs. Electrically, a cycle refers to one full cycle of the encoder’s output waveform: one high pulse and one low pulse. One cycle is equal to 360 electrical degrees.

CPR, then, can refer to the number of lines and windows on the disk, or the number of electrical cycles in one rotation. Native CPR will be the same number in either case, because each line-and-window pair is exactly what generates each electrical cycle.

CPR also gives us the smallest distance that can be measured. Divide the total distance of 360 mechanical degrees by the number of cycles per revolution, and the answer will be mechanical degrees per cycle. For example, with an encoder resolution of 3,600 CPR: 360 degrees per revolution ÷ 3,600 cycles per revolution = 0.1 degree per cycle.

While cycles per revolution is a common term to specify resolution for incremental encoders, some manufacturers use terms like “counts per revolution” (also abbreviated CPR), “pulses per revolution” or “positions per revolution” (both abbreviated PPR), and other phrases. To avoid confusion, we’ll stick with cycles per revolution and CPR.

Resolution Multiplication

The resolution of a disk is tied to physical reality—physical lines on a physical disk. The number of lines, in its most basic form, is the resolution. However, a motion controller can interpret the output waveforms resulting from those lines and produce higher resolutions—from the
same disk.

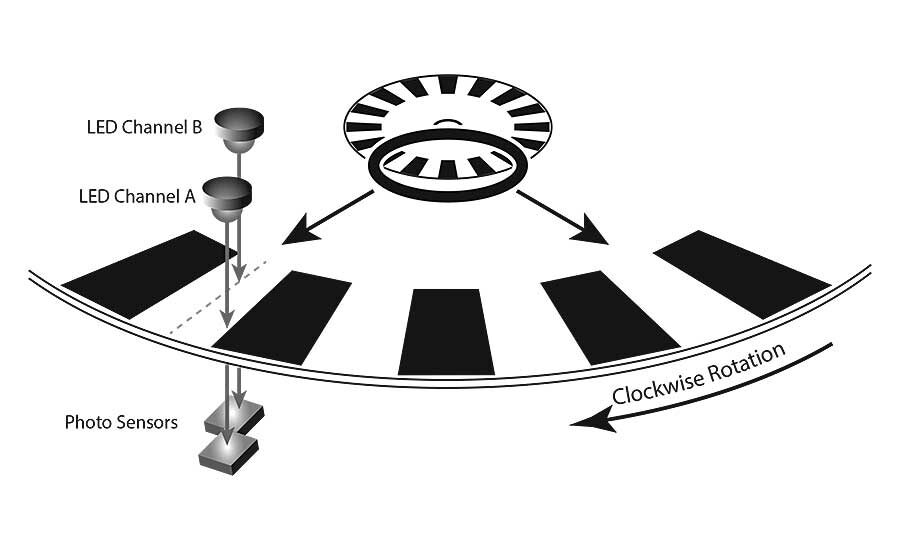
Incremental encoders commonly use quadrature. Manufacturers add another LED and photo sensor, displaced from the first LED by 90 electrical degrees. Note that 90 electrical degrees is a quarter phase or quadrant—which is the origin of the name quadrature.

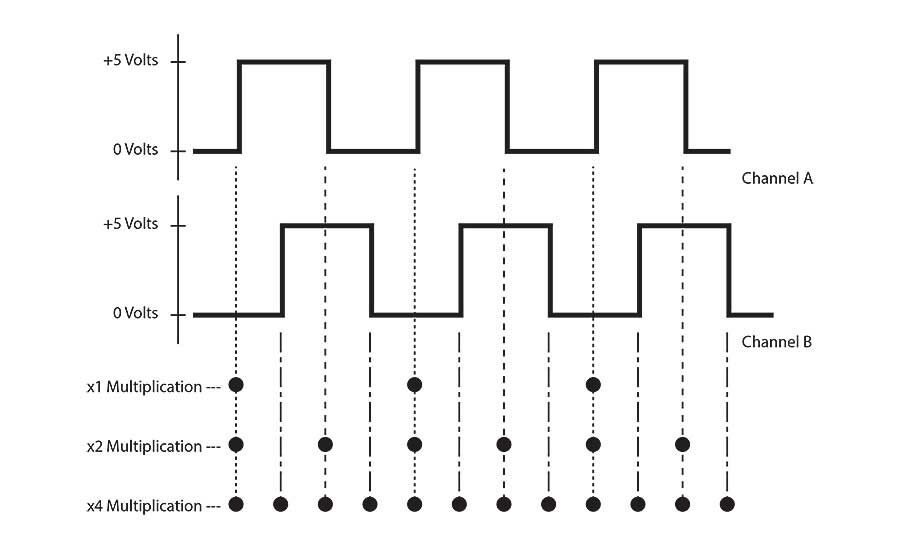
This yields a second output waveform, channel B, shifted in phase from channel A by 90 electrical degrees. Two important results emerge from adding channel B. First, direction can now be determined. For example, “A leads B” can indicate clockwise rotation. More importantly, resolution can be multiplied by a factor of two or four. This is called resolution multiplication. System designers can implement it by using an encoder-to-counter interface chip, such as an LS7183N.

As an example, let’s look at an encoder with 100 lines and windows on its disk. The encoder’s resolution is 100 CPR. If we count the rising edge of each channel A pulse as the disk rotates, we’ll get 100 pulses per revolution. This is the same number as the resolution of 100 CPR, as expected for multiplication by one. If we count each rising edge and each falling edge of channel A, we’ll get 2 pulses per cycle, which adds up to 200 pulses per revolution. If we count each rising edge and falling edge of both channel A and channel B, we’ll get 4 pulses per cycle, for a total of 400 pulses per revolution.

Notice we’re not changing the resolution of the disk; it remains set, as determined by the number of cycles per revolution. But, by decoding the output waveforms in different ways, we are able get up to four times as many pulses per revolution as there are lines on the disk.

Everything we have said so far about resolution also applies to incremental linear encoders. This makes sense; linear encoders use a linear strip that is equivalent to a circular disk that has been cut along a radius and straightened out. The term cycles per inch (CPI) is used for resolution with linear encoders, although lines per inch (LPI) is also sometimes used.

Absolute Encoders and Resolution

Thus far, we’ve discussed incremental optical encoders, whose lines and windows represent relative positions on the disk; each line-and-window pair looks like every other line-and-window pair. They are indistinguishable from each other. What matters are the high and low output transitions as each line and window goes past the sensor.

Absolute encoders operate differently. They output a unique code for each position on the disk—each code is absolute, which means that since it is unlike any other code on the disk, it specifies a unique, absolute position on the disk.

Resolution for absolute encoders is defined as the number of positions per revolution as the disk rotates through 360 degrees. Sometimes, the equivalent term codes per revolution
is used.

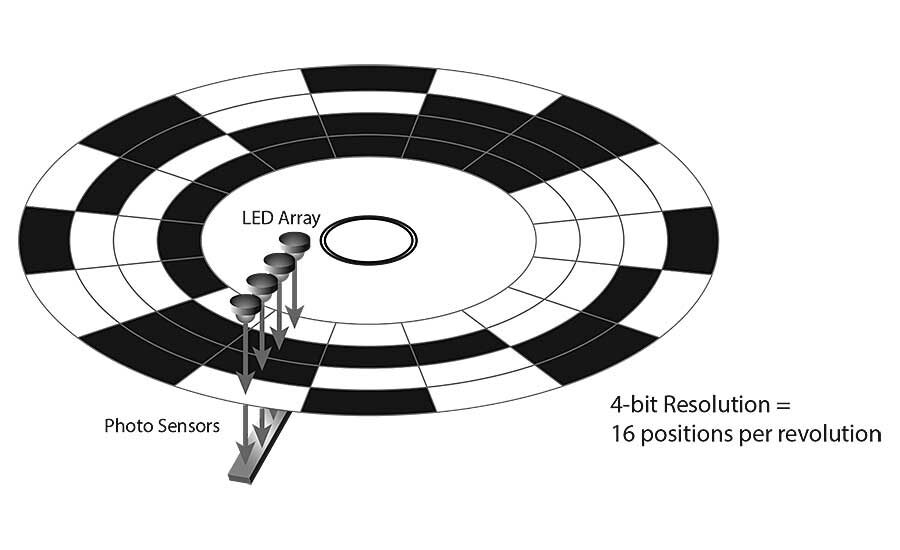
You will often see the resolution of an absolute encoder specified in bits. For example, the disk in the drawing on page 62 has four-bit resolution, one bit being produced from each of the four tracks at each position. Higher resolutions would have more tracks. For example, 10-bit resolution would require 10 tracks.

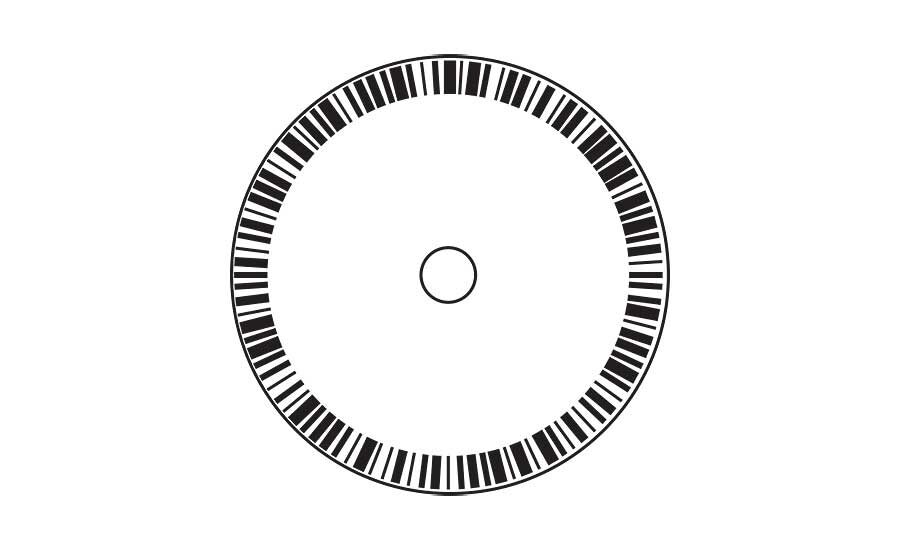
With some designs, each absolute encoder is set at one specific resolution. Some manufacturers, however, take a different approach, and make disks with a single band that contains a unique bar code for each position.

An absolute encoder with a bar code can offer programmable resolution. For example, a 12-bit encoder (4,096 positions per revolution) can be programmed to output from two to 4,096 codes per revolution.

Resolution in bits is related to positions per revolution and degrees of rotation per position. For a 12-bit absolute encoder, each unique position occupies less than 0.1 degree of the disk’s circumference, which is less than 6 arc-minutes.

Absolute encoders don’t use quadrature, so there is no equivalent to resolution multiplication that’s available with incremental encoders.

Scalability: Disk Size and Resolution

Miniaturization is a strong trend in product development. Designers often try to pack more features into increasingly smaller packages. This creates a need for miniature encoders to meet the demand for reduced size. Does reducing encoder size also reduce available resolution?

For traditional encoders, the answer was yes. For traditional encoders, high resolution requires more lines on an encoder disk. If there’s not enough space for the lines to fit, then the only solution is to make a bigger disk. To double the resolution, you have to double the disk’s diameter.

With newer technology, however, manufacturers can increase the resolution of a disk—without increasing disk size. This is called scalability, and it’s ideal for miniaturization.

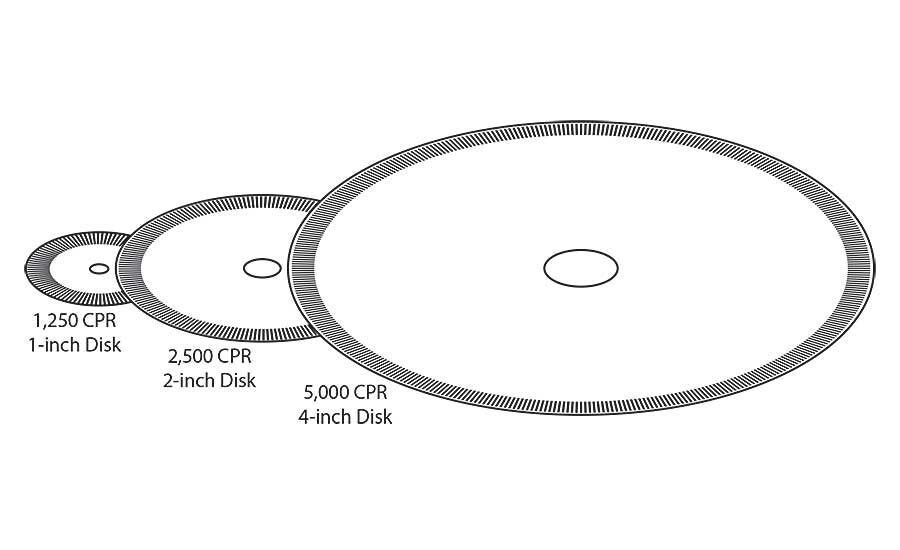
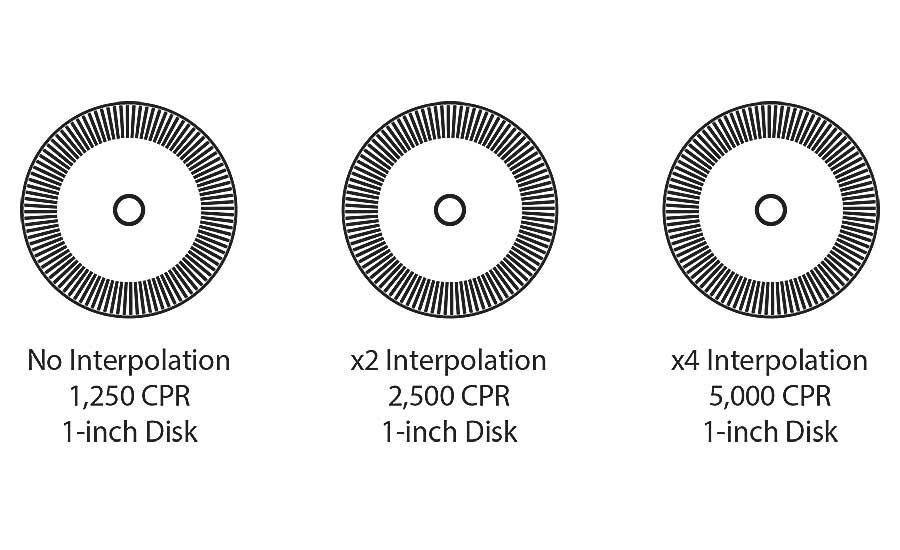
For example, consider a 1-inch disk with 1,250 lines (1,250 CPR). Through the technique of electronic interpolation (signal processing that takes place within the encoder itself), the CPR can be increased to 2,500 CPR using x2 interpolation; and to 5,000 CPR using x4 interpolation. In this example, by using interpolation and scalability, we’ve achieved two increasingly higher resolutions—all from the same small encoder disk. Furthermore, using resolution multiplication, the 5,000 CPR encoder could be decoded to produce 10,000 or 20,000 pulses per revolution.

Not all encoder technologies are equally scalable. Transmissive optical encoders and reflective optical encoders are very scalable. Magnetic encoders are scalable. Capacitive encoders are not easily scalable. Optical encoders are the most flexible and best for miniaturization. With capacitive encoders, however, scalability is much more difficult to accomplish; in most cases, to get a higher resolution, you have to buy a larger encoder—if one is even available.

Interpolation is a wonderful way to achieve scalability, but there are limits. At higher and higher resolutions, jitter may become a problem and waveform symmetry can suffer. If you want higher resolution in a small package, work with your encoder manufacturer. It may be able to provide a custom device that gives you the resolution you desire without signal degradation from jitter or electrical noise.

How Much Resolution Do You Need?

Any particular model of encoder may be available in a range of resolutions. For example, a quick survey of manufacturers might show that a single encoder is available in 20 different resolutions, ranging from 64 to 10,000 CPR.

Is the best practice to always choose the highest resolution? Surprisingly, no. Often it’s better to evaluate your application, and choose the lowest resolution that will satisfy your needs—even if a higher resolution is available. There are many reasons higher resolution may not be the best choice:

• Cost. Higher resolution may cost more.
• Speed. It takes time to read each cycle. Why slow the system down if you don’t have to? Similarly high-velocity applications do not provide enough time to read each cycle.
• Jitter. Sensitive systems may over-respond to high-resolution information.
• Size. In some cases, higher resolutions may have size implications.

Accuracy

When choosing a resolution, a novice designer might look at a specific option in the range of resolutions
available, and say, “No; I need more accuracy than that.” What the designer may really mean is, “I need more resolution.”

Encoders are designed to provide feedback about position, which is used for calculations about angle, distance and velocity. When you command a system to move and then stop at a specific position, you might wonder: Is the encoder reporting from the exact target position? Or, has it gone beyond the target or stopped short of it?

Accuracy is the term used to describe the difference between target position and actual position. In an ideal world, they would be the same—but in the real world, there are variations. The actual position—where the encoder really is—might be off from the target position by a small amount, as indicated by the range in the encoder’s accuracy specification.

Measuring encoder accuracy involves a meticulous procedure that requires sophisticated, well-calibrated equipment. For example, you can measure a medium-accuracy encoder by using a second, highly accurate “calibration” encoder. If you record target vs. actual for each encoder position through one revolution, then evaluate your results, you can determine the accuracy of the encoder under test.

For rotary encoders, accuracy is measured in degrees, arc-minutes or arc-seconds. Which units are used depends upon the encoder being measured. Degrees might be sufficient for a low-accuracy encoder; fractions of a degree or arc-minutes are suitable for encoders with medium accuracy; while arc-seconds might be used for ultra-high accuracy encoders.

For example, one manufacturer might list the “typical accuracy” of an absolute optical shaft encoder as 0.18 degree, which is equal to 10.8 arc-minutes. However, a different
manufacturer of another encoder, an optical incremental shaftless model, might specify the unit’s “position error” as 10 arc-minutes. This manufacturer uses the term position error for accuracy, measured in arc-minutes. It’s the angular difference between the actual shaft position and the position indicated by the encoder cycle count.

The typical accuracy is similar for both encoders, approximately 0.18 degrees or 10 arc-minutes.

Encoder Specs vs. System Accuracy

You may consider accuracy specifications for an encoder you’re evaluating, but accuracy doesn’t end there. Encoders are usually part of a larger motion control system. The non-encoder parts of that system can dramatically affect overall system accuracy. Encoder manufacturers control some of the factors that affect accuracy, while end users control application-specific factors.

Manufacturers influence the accuracy of their encoders by how the pattern is placed on the disk (centered or eccentric); how the hub is mounted to the disk; how the disk is mounted to the shaft; and how the optics are aligned.

End users influence the accuracy of encoders by how the encoder disk is mounted to the motor shaft (for encoder kits); how the encoder
module is mounted (for encoder kits); how the encoder is coupled to the system (for shafted encoders); the stability and rigidity of the mounting structure; gear tolerances and backlash; play in the motor bearings; axial, radial, side-to-side and other motions of mechanical parts; and vibration, temperature, metal fatigue, corrosion and other factors.

With so many variables affecting the performance of an encoder, it’s easy to see how variations in encoder accuracy may be only a small fraction of the total system accuracy.

How Much Accuracy Do You Need?

It’s important to remember that the overall system may be far less accurate than the encoder.

In applications with low system accuracy, all that’s required for encoder accuracy may be monotonicity—as the encoder turns, the count constantly increases or constantly decreases. A low-accuracy encoder can cost less, and as long it provides a reliable, monotonic count, it may be all you need.

As total system accuracy increases, an encoder with medium accuracy might be required. For most applications, encoder accuracy in the range of 0.1 degree, or 8 to 10 arc-minutes, is sufficient.

For applications with extremely close tolerances, high-accuracy encoders with specifications in arc-seconds are available—but with the increase in accuracy, there will be a corresponding increase in cost.

Resolution and Accuracy

We’re now in a position to clear up the common confusion between resolution and accuracy. Let’s consider a manufacturer that offers two versions of a magnetic absolute encoder, one with 12-bit resolution and the other with 10-bit resolution. The 12-bit encoder can report 4,096 positions per revolution, which is four times as many as the 10-bit encoder’s 1,024 positions.

Starting at zero, here are the first nine positions, in degrees, that the 12-bit encoder could report as its disk rotates (some digits omitted for clarity): 0, 0.09, 0.18, 0.27, 0.351562, 0.45, 0.54, 0.63 and 0.703125. For the same amount of rotation, the 10-bit encoder could report the following positions: 0, 0.351562 and 0.703125. In short, the 12-bit encoder is reporting its fourth reading by the time the 10-bit encoder reports its very first reading.

So which encoder is more accurate? Here is what the manufacturer states in the encoder’s data sheet: “While the accuracy is the same for both encoders, the 12-bit version provides higher resolution.”

The accuracy is the same. This example shows that accuracy and resolution are not related to each other. One term—accuracy—describes target position vs. actual position. The other term—resolution—describes how finely a disk is divided. These are independent properties.

If our novice designer needs an encoder that can report positions every tenth of a degree, then the designer needs more resolution, not more accuracy—and the 12-bit encoder would be a good choice.

Precision

To determine the accuracy of an encoder, we can rotate the encoder through one revolution of 360 degrees and note the accuracy—the angular difference between target position and actual position—at each encoder count location.

What happens if we go around a second time and measure accuracy again? Do we get the same position error at each location? How about after a third, fourth or fifth rotation? Is the position error repeatable, or does it vary?

Precision is the term that describes repeatability of measurements. It’s the amount that successive measurements differ from each other. Consider arrows shot by two archers in a competition (figure 12). Which archer is more accurate?

Surprisingly, the average accuracy is similar for both targets. The average position of all the arrows on the left is in the center of the bullseye, the same as the tight grouping of arrows on the right. The difference between the two lies in the precision of the shots. The group on the left is accurate, but not precise. The group on the right is both accurate and precise.

Now let’s look at arrows shot by two more archers (see figure 13). Which archer is more precise?

The precision is the same for both archers. The arrows on the left are precise—but they are not accurate. The group on the right is, again, both accurate and precise.

Putting Precision to Work

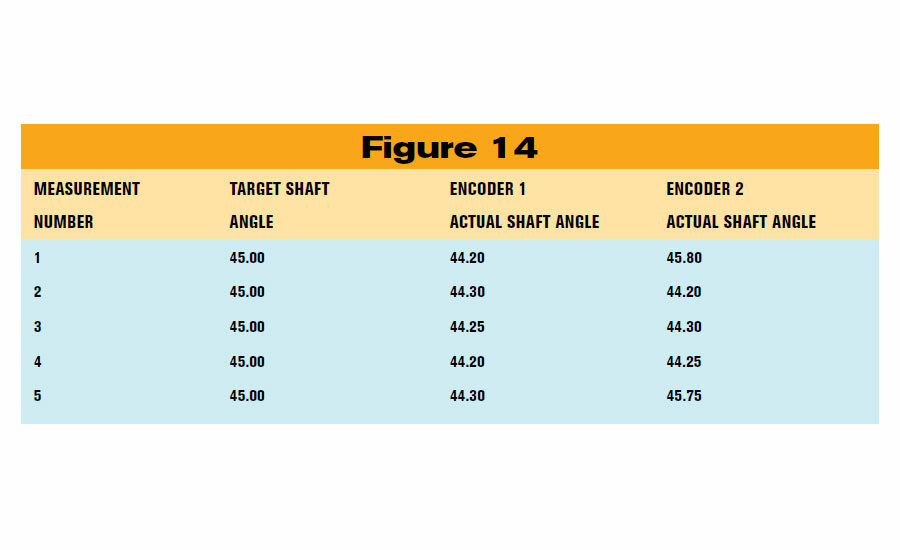
Precision, then, is the amount that successive measurements differ from each other. An encoder that has position errors which are repeatable may have good precision, even though it may not be perfectly accurate. In this case, the precision can be used to compensate for the inaccuracy of the encoder. For example, let’s look at successive measurements made for two encoders. (See figure 14.) The target shaft angle is 45 degrees.

The position error is about 0.75 degree for each encoder, but while Encoder 2’s errors follow no repeatable pattern, Encoder 1 is more precise—its error is always -0.75 degree, on average. Encoder 1’s precision can be put to good use. The error can be tabulated at each position, and those measurements can be used to compensate the encoder’s reported position.

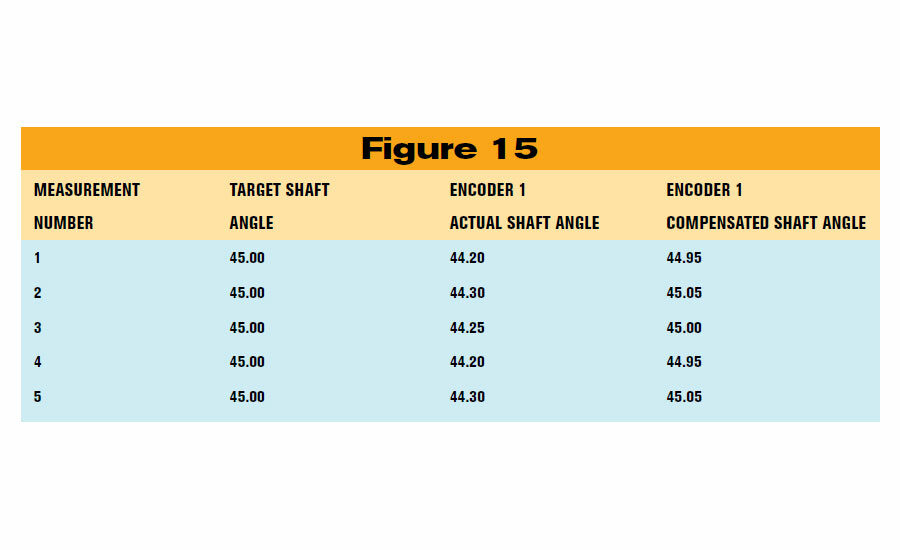
For example, if we add 0.75 degree to each of the earlier measurements from Encoder 1, it will now report a compensated position that is within 0.05 degree of the target position, which is much more accurate than its uncompensated average readings of -0.75 degree. (See figure 15.) In fact, this compensation technique is used when manufacturers produce high-accuracy encoders. These encoders are manufactured to standards that ensure that whatever error they have, it’s repeatable. Their precision is used to create a lookup table for error compensation, which is applied to each position the encoder reports.

Precision of an Entire System

The concept of precision applies to every component of a motion control system, not just the encoder. For example, consider a cut-to-length application. An encoder is attached to a motor that drives a ballscrew and actuator, which positions wire for cutting.

Suppose the system is set to cut the wire at exactly 12.00 inches. After the first four wires are cut, they are measured, with the following results: 11.81 inches, 11.82 inches, 11.80 inches and 11.81 inches.

The wires are consistently about 0.2 inches too short. Where is the error coming from? It could be from anywhere—or everywhere—in the system: the encoder, the motor, or play in the threads of the ballscrew or in the bearings of the linear slide.

Because the difference between readings is small, the system has good precision. This can be used to calibrate the application; 0.20 inches can be added to the final target position of 12.00 inches, to end up at a compensated position of 12.20 inches. When the wires are then cut, they will be very close to the desired length of 12.00 inches.